Tree-Seed Algorithm
Tree-Seed Algorithm (TSA) is a population-based heuristic search algorithm recently proposed to solve continuous optimization problems[1].
In TSA, trees and seeds represents the possible solution for the optimization problem.
The tree population is called as the stand and the number of trees in a stand is a control parameter for TSA (known as population size in the swarm intelligence or evolutionary computation algorithms).
There are two peculiar control parameters in TSA, whose names are search tendency-ST and number of seeds which will be produced for each tree-NS.
Two update equations are used in TSA and ST controls the selection of the update equation to produce seed for the tree.
NS is used to determine the number of seeds which will be produced in TSA.
NS and ST have been analyzed and 0.1 is suitable for ST and NS can be between 10% and 25% of the stand [1] but these parameters should be tuned by depending on the characteristics of the optimization problem.
The Working Diagram of TSA
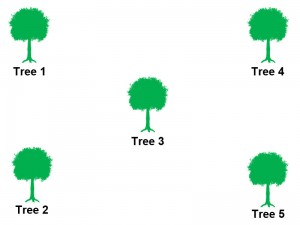
(a) is the initialization of TSA. Trees are scattered to the search space and the fitness of the trees are calculated by using objective function specific for the optimization problem.
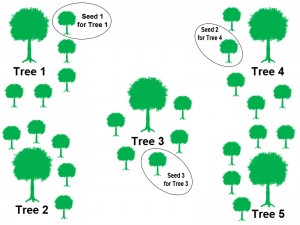
(b) is the seed production mechanism. The number of seeds for each tree is changeable. In the diagram, five seeds are produced for each tree and the best seeds are compared with the parent tree.
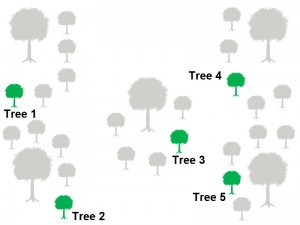
(c) is the replacement procedure. If fitness of the best seed is better than the fitness of its parent tree, the parent tree is removed from the stand and its best seed is located to stand.
The termination condition is maximum number of function evaluations (Max_FEs) for TSA. Because the number of seeds is changeable for each tree, Max_FEs should be used in TSA instead of iteration time.
Future Directions for TSA
The TSA was proposed to solve unconstrained optimization problems. I suggest some ideas on TSA for the researchers:
Implementations of TSA
Matlab Implementation of TSA
Java Implementation of TSA
I, my PhD students and my colleagues also study on TSA to solve constrained optimization and discrete optimization problems. For national or international collaboration, you can contact with me
[1] Kiran M.S., 2015, TSA:Tree-Seed Algorithm for Continuous Optimization, Expert Systems with Applications, Volume 11, pp. 6686-6698.
The Working Diagram of TSA
(a) |
(b) |
(c) |
(a) is the initialization of TSA. Trees are scattered to the search space and the fitness of the trees are calculated by using objective function specific for the optimization problem.
(b) is the seed production mechanism. The number of seeds for each tree is changeable. In the diagram, five seeds are produced for each tree and the best seeds are compared with the parent tree.
(c) is the replacement procedure. If fitness of the best seed is better than the fitness of its parent tree, the parent tree is removed from the stand and its best seed is located to stand.
The termination condition is maximum number of function evaluations (Max_FEs) for TSA. Because the number of seeds is changeable for each tree, Max_FEs should be used in TSA instead of iteration time.
Future Directions for TSA
The TSA was proposed to solve unconstrained optimization problems. I suggest some ideas on TSA for the researchers:
- The performance of TSA on high dimensional problems can be improved by considering different update mechanisms.
- The binary versions of TSA can be developed for binary optimization.
- The discrete versions of TSA can be developed
- The TSA can be modified for constrained optimization.
- The TSA can be applied to solve optimization problems in different field of research.
- Current control parameters can be analyzed or new control parameters can be added to TSA to improve its performance.
Implementations of TSA
Matlab Implementation of TSA
Java Implementation of TSA
I, my PhD students and my colleagues also study on TSA to solve constrained optimization and discrete optimization problems. For national or international collaboration, you can contact with me
[1] Kiran M.S., 2015, TSA:Tree-Seed Algorithm for Continuous Optimization, Expert Systems with Applications, Volume 11, pp. 6686-6698.
